Lượng giác là một nhánh quan trọng của toán học, đặc biệt trong chương trình Toán lớp 10 và 11 (sách Cánh Diều), với ứng dụng rộng rãi trong vật lý, kỹ thuật, và đời sống. Các công thức lượng giác giúp giải quyết bài toán về góc, cạnh trong tam giác, và phân tích hàm số lượng giác.
Giá trị lượng giác của các góc đặc biệt
Các góc đặc biệt (0°, 30°, 45°, 60°, 90°) có giá trị lượng giác cố định, là nền tảng để tính toán nhanh và áp dụng vào bài toán.
| Góc (α) | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin α | 0 | ( \frac{1}{2} ) | ( \frac{\sqrt{2}}{2} ) | ( \frac{\sqrt{3}}{2} ) | 1 |
| cos α | 1 | ( \frac{\sqrt{3}}{2} ) | ( \frac{\sqrt{2}}{2} ) | ( \frac{1}{2} ) | 0 |
| tan α | 0 | ( \frac{\sqrt{3}}{3} ) | 1 | ( \sqrt{3} ) | ∞ |
| cot α | ∞ | ( \sqrt{3} ) | 1 | ( \frac{\sqrt{3}}{3} ) | 0 |
Mẹo ghi nhớ:
- Sin tăng, cos giảm: Sin tăng từ 0 (0°) đến 1 (90°), cos giảm từ 1 (0°) đến 0 (90°).
- Căn bậc hai: Giá trị sin, cos có dạng ( \frac{\sqrt{n}}{2} ), với ( n = 0, 1, 2, 3, 4 ).
- Tan và cot: ( \tan \alpha = \frac{\sin \alpha}{\cos \alpha} ), ( \cot \alpha = \frac{\cos \alpha}{\sin \alpha} ).
Ví dụ minh họa:
Tính ( \sin 30^\circ + \cos 60^\circ ).
[ \sin 30^\circ = \frac{1}{2}, \quad \cos 60^\circ = \frac{1}{2} \implies \sin 30^\circ + \cos 60^\circ = \frac{1}{2} + \frac{1}{2} = 1. ]
Công thức lượng giác cơ bản
Công thức cung liên quan
Các công thức này liên kết giá trị lượng giác của các góc đối, bù, phụ, hoặc hơn kém nhau.
- Cung đối:
[ \sin(-x) = -\sin x, \quad \cos(-x) = \cos x, \quad \tan(-x) = -\tan x. ] - Cung bù nhau (( \alpha + \beta = 180^\circ )):
[ \sin(180^\circ – x) = \sin x, \quad \cos(180^\circ – x) = -\cos x, \quad \tan(180^\circ – x) = -\tan x. ] - Cung phụ nhau (( \alpha + \beta = 90^\circ )):
[ \sin(90^\circ – x) = \cos x, \quad \cos(90^\circ – x) = \sin x, \quad \tan(90^\circ – x) = \cot x. ] - Cung hơn kém (\pi/2):
[ \sin\left(x \pm \frac{\pi}{2}\right) = \pm \cos x, \quad \cos\left(x \pm \frac{\pi}{2}\right) = \mp \sin x. ]
Mẹo ghi nhớ:
- Cung đối: “Sin, tan đổi dấu, cos giữ nguyên”.
- Cung bù: “Sin giữ, cos đổi, tan đổi”.
- Cung phụ: “Sin thành cos, cos thành sin, tan thành cot”.
Ví dụ minh họa:
Tính ( \sin 150^\circ ).
[ \sin 150^\circ = \sin(180^\circ – 30^\circ) = \sin 30^\circ = \frac{1}{2}. ]
Công thức cơ bản liên hệ giữa các hàm
- Công thức Pythagoras lượng giác:
[ \sin^2 x + \cos^2 x = 1. ] [ 1 + \tan^2 x = \frac{1}{\cos^2 x} \text{ (hay } \sec^2 x\text{)}. ] [ 1 + \cot^2 x = \frac{1}{\sin^2 x} \text{ (hay } \csc^2 x\text{)}. ] - Liên hệ giữa tan và cot:
[ \tan x = \frac{\sin x}{\cos x}, \quad \cot x = \frac{\cos x}{\sin x}, \quad \tan x \cdot \cot x = 1. ]
Mẹo ghi nhớ:
- Pythagoras: “Sin vuông cộng cos vuông bằng 1”.
- Tan và cot: “Tan là sin chia cos, cot là cos chia sin”.
Ví dụ minh họa:
Cho ( \sin x = \frac{3}{5} ), tính ( \cos x ).
[ \sin^2 x + \cos^2 x = 1 \implies \left(\frac{3}{5}\right)^2 + \cos^2 x = 1 \implies \frac{9}{25} + \cos^2 x = 1 \implies \cos^2 x = \frac{16}{25} \implies \cos x = \pm \frac{4}{5}. ]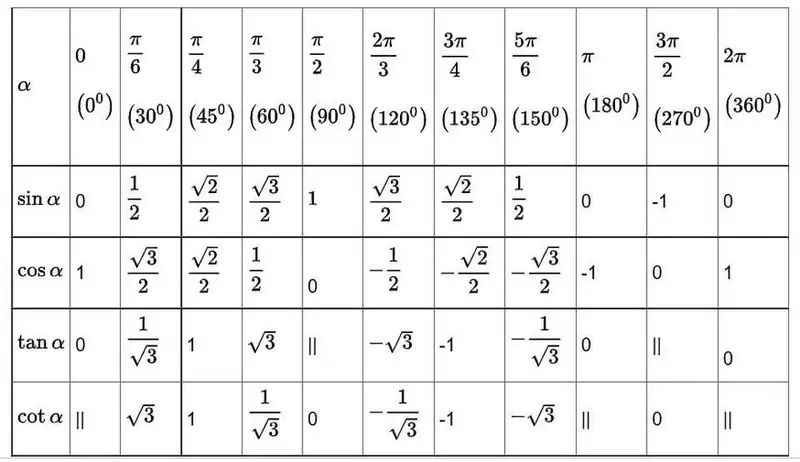
Công thức cộng
Dùng để biểu diễn hàm lượng giác của tổng hoặc hiệu hai góc.
- Tổng:
[ \sin(A + B) = \sin A \cos B + \cos A \sin B. ] [ \cos(A + B) = \cos A \cos B – \sin A \sin B. ] [ \tan(A + B) = \frac{\tan A + \tan B}{1 – \tan A \tan B}. ] - Hiệu:
[ \sin(A – B) = \sin A \cos B – \cos A \sin B. ] [ \cos(A – B) = \cos A \cos B + \sin A \sin B. ] [ \tan(A – B) = \frac{\tan A – \tan B}{1 + \tan A \tan B}. ]
Mẹo ghi nhớ:
- Sin cộng: “Sin cos cộng cos sin”.
- Cos cộng: “Cos cos trừ sin sin”.
- Tan cộng: “Cộng tan chia (1 trừ tích tan)”.
- Hiệu đổi dấu theo quy tắc: “Cộng thành trừ, trừ thành cộng”.
Ví dụ minh họa:
Tính ( \sin 75^\circ ).
[ \sin 75^\circ = \sin(45^\circ + 30^\circ) = \sin 45^\circ \cos 30^\circ + \cos 45^\circ \sin 30^\circ = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} = \frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} = \frac{\sqrt{6} + \sqrt{2}}{4}. ]
Công thức nhân đôi
Biểu diễn hàm lượng giác của ( 2x ) qua ( x ).
- Sin nhân đôi:
[ \sin 2x = 2 \sin x \cos x. ] - Cos nhân đôi:
[ \cos 2x = \cos^2 x – \sin^2 x = 2\cos^2 x – 1 = 1 – 2\sin^2 x. ] - Tan nhân đôi:
[ \tan 2x = \frac{2 \tan x}{1 – \tan^2 x}. ]
Mẹo ghi nhớ:
- Sin 2x: “Gấp đôi sin cos”.
- Cos 2x: Có ba dạng, nhớ “cos vuông trừ sin vuông” hoặc chuyển về sin, cos đơn.
- Tan 2x: “Gấp đôi tan chia (1 trừ tan vuông)”.
Ví dụ minh họa:
Cho ( \cos x = \frac{4}{5} ), tính ( \sin 2x ).
[ \sin^2 x = 1 – \cos^2 x = 1 – \left(\frac{4}{5}\right)^2 = 1 – \frac{16}{25} = \frac{9}{25} \implies \sin x = \pm \frac{3}{5}. ]
[ \sin 2x = 2 \sin x \cos x = 2 \cdot \frac{3}{5} \cdot \frac{4}{5} = \frac{24}{25}. ]
Công thức hạ bậc
Chuyển các hàm ( \sin^2 x, \cos^2 x, \tan^2 x ) về dạng ( \sin 2x, \cos 2x ).
- [ \sin^2 x = \frac{1 – \cos 2x}{2}. ]
- [ \cos^2 x = \frac{1 + \cos 2x}{2}. ]
- [ \tan^2 x = \frac{1 – \cos 2x}{1 + \cos 2x}. ]
Mẹo ghi nhớ:
- Sin vuông: “1 trừ cos 2x chia 2”.
- Cos vuông: “1 cộng cos 2x chia 2”.
- Tan vuông: Tỷ số của sin vuông và cos vuông.
Ví dụ minh họa:
Biểu diễn ( \sin^2 30^\circ ) qua ( \cos 60^\circ ).
[ \sin^2 30^\circ = \frac{1 – \cos 60^\circ}{2} = \frac{1 – \frac{1}{2}}{2} = \frac{\frac{1}{2}}{2} = \frac{1}{4}. ]
Công thức tổng thành tích
Chuyển tổng hoặc hiệu các hàm lượng giác thành tích.
- [ \sin A + \sin B = 2 \sin\left(\frac{A + B}{2}\right) \cos\left(\frac{A – B}{2}\right). ]
- [ \sin A – \sin B = 2 \cos\left(\frac{A + B}{2}\right) \sin\left(\frac{A – B}{2}\right). ]
- [ \cos A + \cos B = 2 \cos\left(\frac{A + B}{2}\right) \cos\left(\frac{A – B}{2}\right). ]
- [ \cos A – \cos B = -2 \sin\left(\frac{A + B}{2}\right) \sin\left(\frac{A – B}{2}\right). ]
Mẹo ghi nhớ:
- Tổng sin: “2 sin trung bình nhân cos hiệu nửa”.
- Hiệu cos: “-2 sin trung bình nhân sin hiệu nửa”.
- Trung bình là ( \frac{A + B}{2} ), hiệu nửa là ( \frac{A – B}{2} ).
Ví dụ minh họa:
Tính ( \sin 75^\circ + \sin 15^\circ ).
[ \sin 75^\circ + \sin 15^\circ = 2 \sin\left(\frac{75^\circ + 15^\circ}{2}\right) \cos\left(\frac{75^\circ – 15^\circ}{2}\right) = 2 \sin 45^\circ \cos 30^\circ = 2 \cdot \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} = \sqrt{6}. ]
Công thức tích thành tổng
Chuyển tích các hàm lượng giác thành tổng hoặc hiệu.
- [ \sin A \cos B = \frac{1}{2} [\sin(A + B) + \sin(A – B)]. ]
- [ \cos A \sin B = \frac{1}{2} [\sin(A + B) – \sin(A – B)]. ]
- [ \cos A \cos B = \frac{1}{2} [\cos(A + B) + \cos(A – B)]. ]
- [ \sin A \sin B = -\frac{1}{2} [\cos(A + B) – \cos(A – B)]. ]
Mẹo ghi nhớ:
- Sin cos: “Nửa tổng sin cộng và hiệu”.
- Cos cos: “Nửa tổng cos cộng và hiệu”.
- Sin sin: “Nửa âm hiệu cos cộng và hiệu”.
Ví dụ minh họa:
Tính ( \sin 30^\circ \cos 60^\circ ).
[ \sin 30^\circ \cos 60^\circ = \frac{1}{2} [\sin(30^\circ + 60^\circ) + \sin(30^\circ – 60^\circ)] = \frac{1}{2} [\sin 90^\circ + \sin(-30^\circ)] = \frac{1}{2} [1 – \sin 30^\circ] = \frac{1}{2} \left[1 – \frac{1}{2}\right] = \frac{1}{4}. ]
Mẹo học và ghi nhớ
- Học bảng góc đặc biệt: Thuộc lòng bảng giá trị lượng giác của 0°, 30°, 45°, 60°, 90° để tính nhanh.
- Nhóm công thức: Chia thành các nhóm:
- Cơ bản: Pythagoras, tan-cot.
- Cung liên quan: Đối, bù, phụ.
- Công thức phức tạp: Cộng, nhân đôi, hạ bậc, tổng-tích.
- Liên tưởng hình học: Gắn công thức với vòng tròn lượng giác hoặc tam giác vuông để hiểu ý nghĩa.
- Luyện tập ví dụ: Làm bài tập với góc đặc biệt để quen thuộc.
- Sơ đồ tư duy: Vẽ sơ đồ phân chia:
- Cơ bản: Sin vuông + cos vuông = 1.
- Cung liên quan: Đối, bù, phụ.
- Phức tạp: Cộng, nhân đôi, hạ bậc, tổng-tích.
Bài tập áp dụng
Bài tập 1: Tính ( \cos 105^\circ ).
Lời giải:
[ \cos 105^\circ = \cos(60^\circ + 45^\circ) = \cos 60^\circ \cos 45^\circ – \sin 60^\circ \sin 45^\circ = \frac{1}{2} \cdot \frac{\sqrt{2}}{2} – \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{4} – \frac{\sqrt{6}}{4} = \frac{\sqrt{2} – \sqrt{6}}{4}. ]
Bài tập 2: Chứng minh ( \sin^2 x + \cos^2 x = 1 ).
Lời giải:
Dùng công thức hạ bậc:
[ \sin^2 x = \frac{1 – \cos 2x}{2}, \quad \cos^2 x = \frac{1 + \cos 2x}{2}. ]
[ \sin^2 x + \cos^2 x = \frac{1 – \cos 2x}{2} + \frac{1 + \cos 2x}{2} = \frac{1 – \cos 2x + 1 + \cos 2x}{2} = \frac{2}{2} = 1. ]
Bài tập 3: Biểu diễn ( \cos 2x ) qua ( \sin x ).
Lời giải:
[ \cos 2x = 1 – 2\sin^2 x. ]
Bài tập 4: Tính ( \sin 15^\circ – \sin 75^\circ ).
Lời giải:
[ \sin 75^\circ – \sin 15^\circ = 2 \cos\left(\frac{75^\circ + 15^\circ}{2}\right) \sin\left(\frac{75^\circ – 15^\circ}{2}\right) = 2 \cos 45^\circ \sin 30^\circ = 2 \cdot \frac{\sqrt{2}}{2} \cdot \frac{1}{2} = \frac{\sqrt{2}}{2}. ]
Kết luận
Các công thức lượng giác là công cụ quan trọng để giải bài toán về góc, cạnh, và hàm số. Nắm vững các công thức cơ bản, cung liên quan, cộng, nhân đôi, hạ bậc, tổng thành tích sẽ giúp bạn giải bài tập dễ dàng và nhanh chóng. Với mẹo ghi nhớ, ví dụ minh họa, và bài tập áp dụng, bạn có thể tự tin sử dụng lượng giác trong học tập và ứng dụng thực tế. Hãy luyện tập thường xuyên để ghi nhớ lâu dài!
Xem thêm:
- Hành Tinh Đôi Đông Chí & chúng hoạt động ra sao?
- Mặt Trời mọc ở hướng nào? Lặn hướng nào? Cùng tìm hiểu và khám phá
- Cách dùng “cho nên” và “cho lên” chuẩn nhất
- Cách dùng “xẻ” và “sẻ” chuẩn nhất
- Lý thuyết công và công suất: Giải thích dễ hiểu
- Lý thuyết quyền công dân và nghĩa vụ cơ bản của công dân (GDCD 6)
- 50 bài tập đạo hàm cơ bản theo quy tắc có lời giải
- Hằng đẳng thức đáng nhớ Toán 8 – Cánh Diều chi tiết

